Back 40: Engineer's corner

By Philip Kedrowski Redleaf Consulting
A contractor walked into my office the other day and asked, “What do you think about the Mooney wall system?”
“What’s a Mooney wall system? ” I asked.
He explained that it’s a technique for furring out a standard wall to add room for additional insulation. This led into a broader conversation about numerous wall assemblies, and we finally got to the heart of the question: How do we compare these different walls on an apples-to-apples basis so he could make the best choice on what to recommend to his clients?
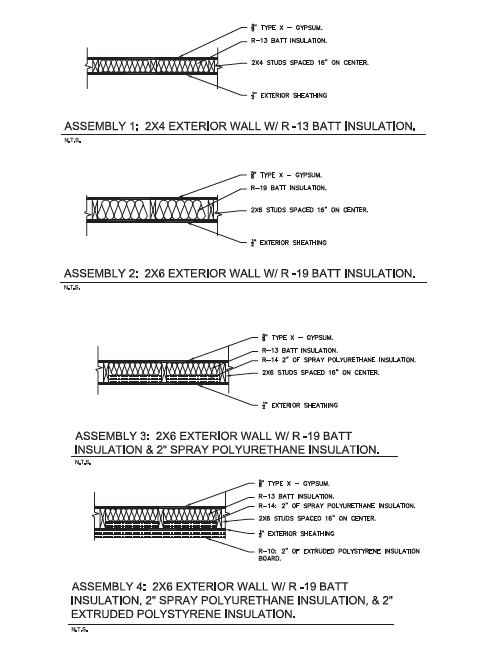
Here, I will show you a heat transfer comparison of four common exterior wall assemblies. Illustrations of these assemblies are shown in Figure 1. The first step in comparing these four wall assemblies is to calculate the overall resistance to heat transfer (R-value) for each.
Figure 1
Since all four assemblies have interior gypsum and exterior wood sheathing, I’ll exclude them to simplify the example. Each of these assemblies has components with an R-value stacked atop each other (in series) and side-by-side (in parallel).
The following two equations can be used for determining the total R-value for each condition:

Don’t worry, this isn’t a lecture on heat transfer mathematics. I’m just showing you the equations so you know I’m not pulling this out of thin air. Using these equations, I’ve calculated the following R-values for each assembly.

Notice that Assembly 4 has an overall R-Value three times the overall R-value of Assembly 1. Does that mean it’s three times as good?
In order to answer that question, we need to look at the conductive heat transfer equation.

Using this equation we can calculate the conduction heat transfer (Q) across a wall area. Heat transfer, quantified in British Thermal Units per Hour (BTU/Hr), is directly tied to how much energy your house consumes. Your home’s furnace or boiler is sized to deliver a specific number of BTU’s/Hr. The larger this number, the more money it will cost to heat your home. Therefore, in order to compare wall assemblies, it’s more important to look at reduction in heat transfer than to simply compare R-values.
In Figure 2, I’ve used the conduction heat transfer equation to create a curve showing the percent reduction in heat loss as a function of R-value. Here’s a simple way to think of it: If you have 0 percent reduction in heat loss, you’d be sitting outside and would need a lot of energy to stay warm. On the other hand, if you have 100 percent reduction in heat loss, you could maintain the temperature in your home with no input energy at all.
Figure 2
Notice how the curve rises quickly and then flattens out. This means you get a lot of bang for your buck at the lower R-values. Assembly 1 already achieves a 91 percent reduction in heat loss, but that’s not good enough. As we move to assemblies 2, 3 and 4, we successively get more reduction in heat loss. However, each new percentage of heat loss reduction is harder to achieve.
As mentioned above, Assembly 4 has three times the R-value of Assembly 1, but the plot shows we only get 6 percent more reduction in heat loss. Unfortunately, it’s not three times as good: If we invented an assembly with an R-100, we would only achieve another 2 percent reduction in heat loss over Assembly 4.

Philip Kedrowski, PE, LEED-AP, is owner/engineer of Redleaf Consulting, PLLC. Redleaf is the only engineering company based in Big Sky.